1. 문제요약
1520번: 내리막 길
첫째 줄에는 지도의 세로의 크기 M과 가로의 크기 N이 빈칸을 사이에 두고 주어진다. 이어 다음 M개 줄에 걸쳐 한 줄에 N개씩 위에서부터 차례로 각 지점의 높이가 빈 칸을 사이에 두고 주어진다.
www.acmicpc.net

지도의 각 칸에는 그 지점의 높이가 주어지며 (0, 0) 지점에서 (n-1, m-1) 지점으로 내려가려고 한다. 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 할 때 이동할 수 있는 경로의 수를 구하시오.
2. 문제예제

3. 팩트추출
Fact 1 : 전형적인 BFS 와 DFS 문제인 것처럼 보이지만, 입력의 범위를 보면 완전 탐색 시 시간 초과가 발생할 수 있다. 최대 칸 수가 500 * 500 으로 250000 이며 상하좌우 4방향으로 움직일 수 있으니 4 의 250000 제곱 경우의 수가 존재한다. 경우의 수를 줄일 수 있는 방법을 찾아야 한다.
Fact 2 : 문제 예제를 살펴보면 전체 문제의 답이 작은 부분 문제의 답의 합으로 구성되어 있다. 50 번 지점에서 목적지까지 가는 경로의 수는 45번 지점에서 가는 경로의 수 + 35번 지점에서 가는 경로의 수로 이루어져 있다. 35번 지점이나 30번 지점, 27번 지점은 경로의 수가 하나로 나중에 이 지점을 방문하더라도 계산할 필요가 없다. 즉 DP 문제이다.
Fact 3 : 기존 DFS 나 BFS 에서 사용하던 visited 배열을 응용하여 "해당 지점에서 목적지까지 가는 경로의 수" 로 생각하여 해당 값을 재활용하면 탐색 범위를 줄일 수 있다. 여기서 중요한 점은 DFS 와 BFS 의 visited 배열 활용도가 조금 다르다는 것이다. BFS 는 주변부터 탐색하기 때문에 단순 방문했는지 여부만 파악할 수 있지만 DFS 는 한 가지 경우의 수부터 모두 탐색하고 다시 원래 위치로 돌아오기 때문에 수행 도중 visited 배열을 오염시킨다면 그 경로는 다시 탐색하지 않아도 된다. 4 번 문제 풀이 (수동) 부분에서 자세히 확인한다.
Fact 4 : DP[x][y] 배열을 0 으로 초기화하면 이 경로의 수가 0 인지 노드를 방문하지 않은 것인지 확인이 불가능하다. DP 배열이 visited 배열의 역할도 하기 때문에 -1 로 초기화한다.
4. 문제풀이(수동)
문제 예제 입력 1을 DFS 알고리즘 + DP 방식으로 문제를 풀었을 때 애니메이션이다.
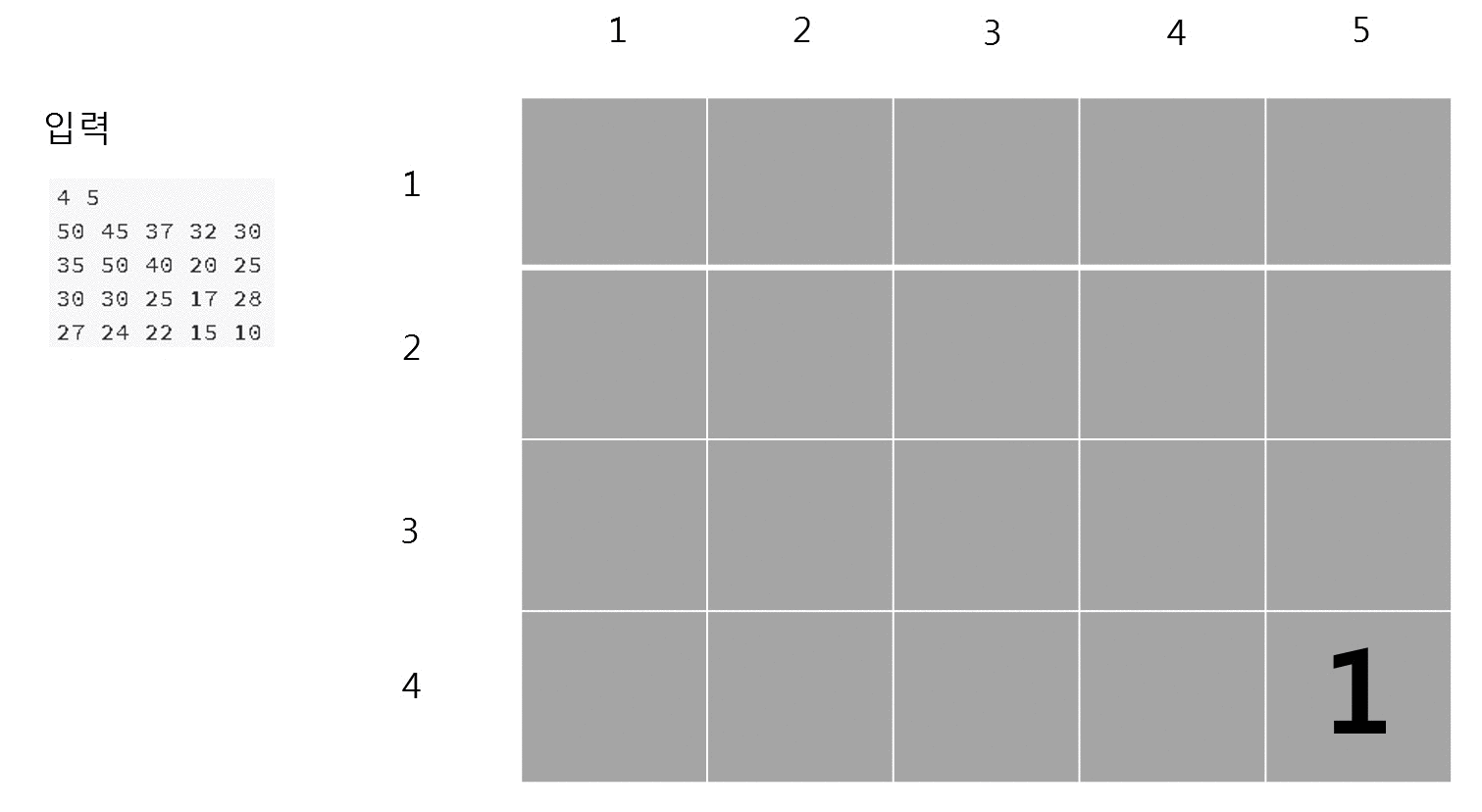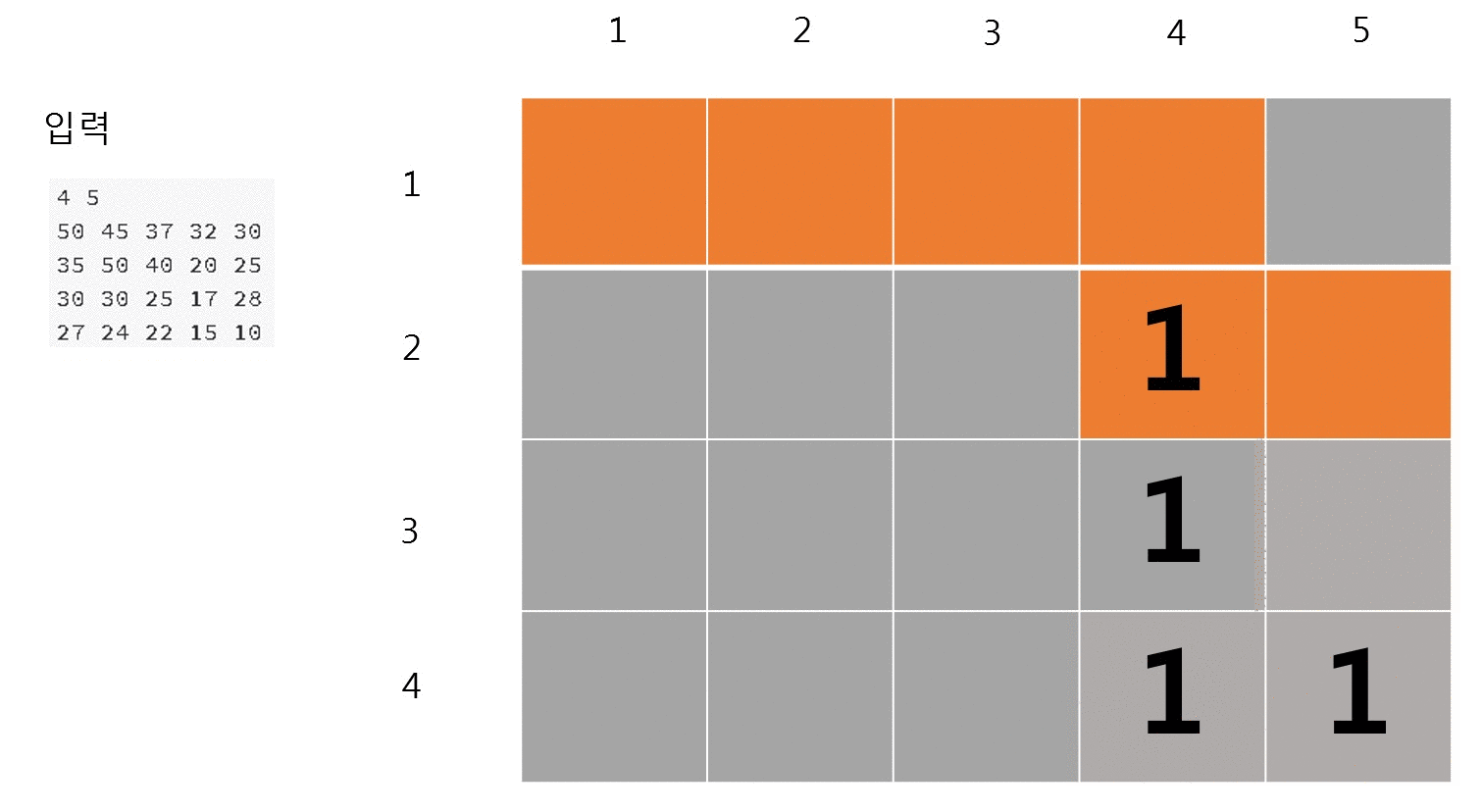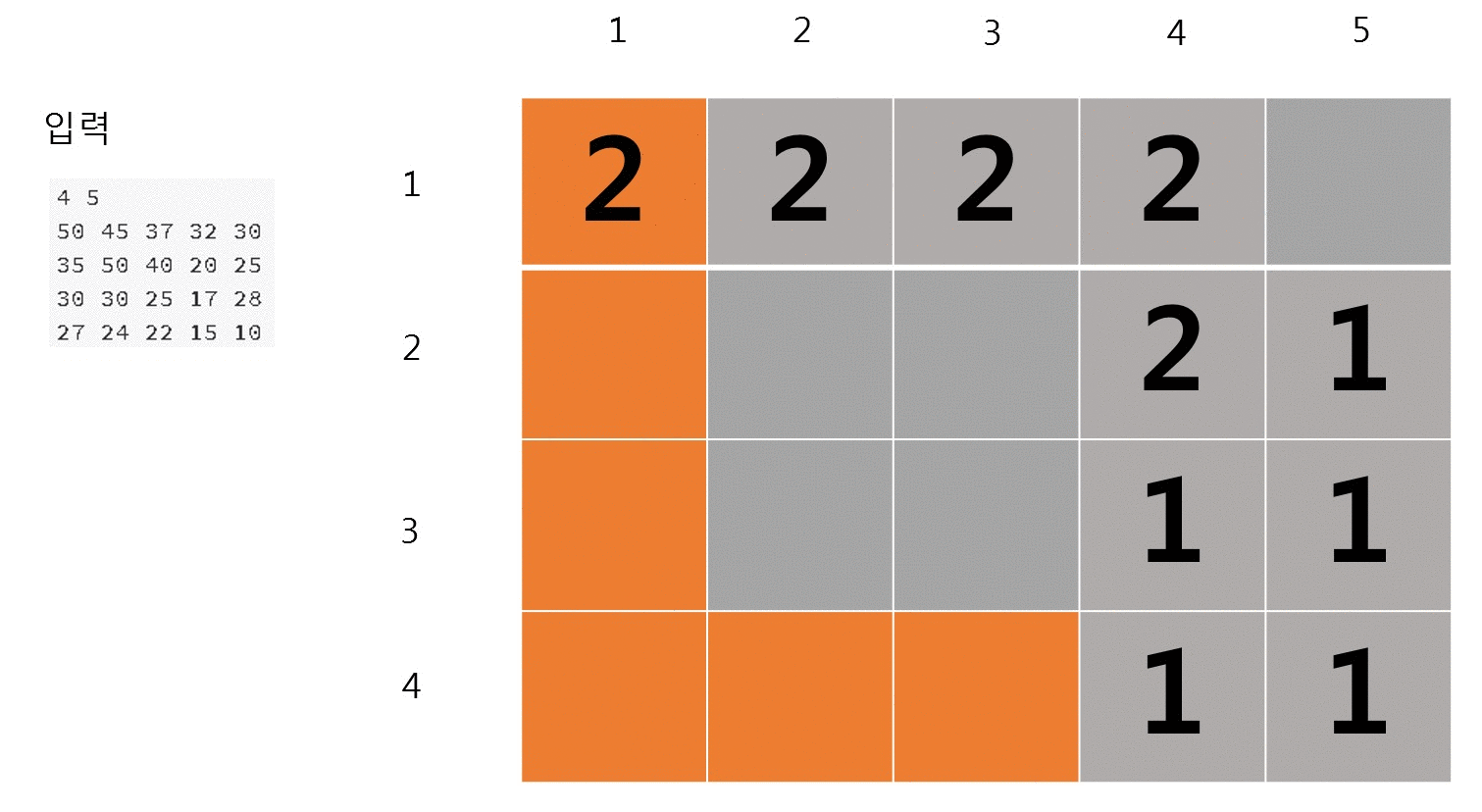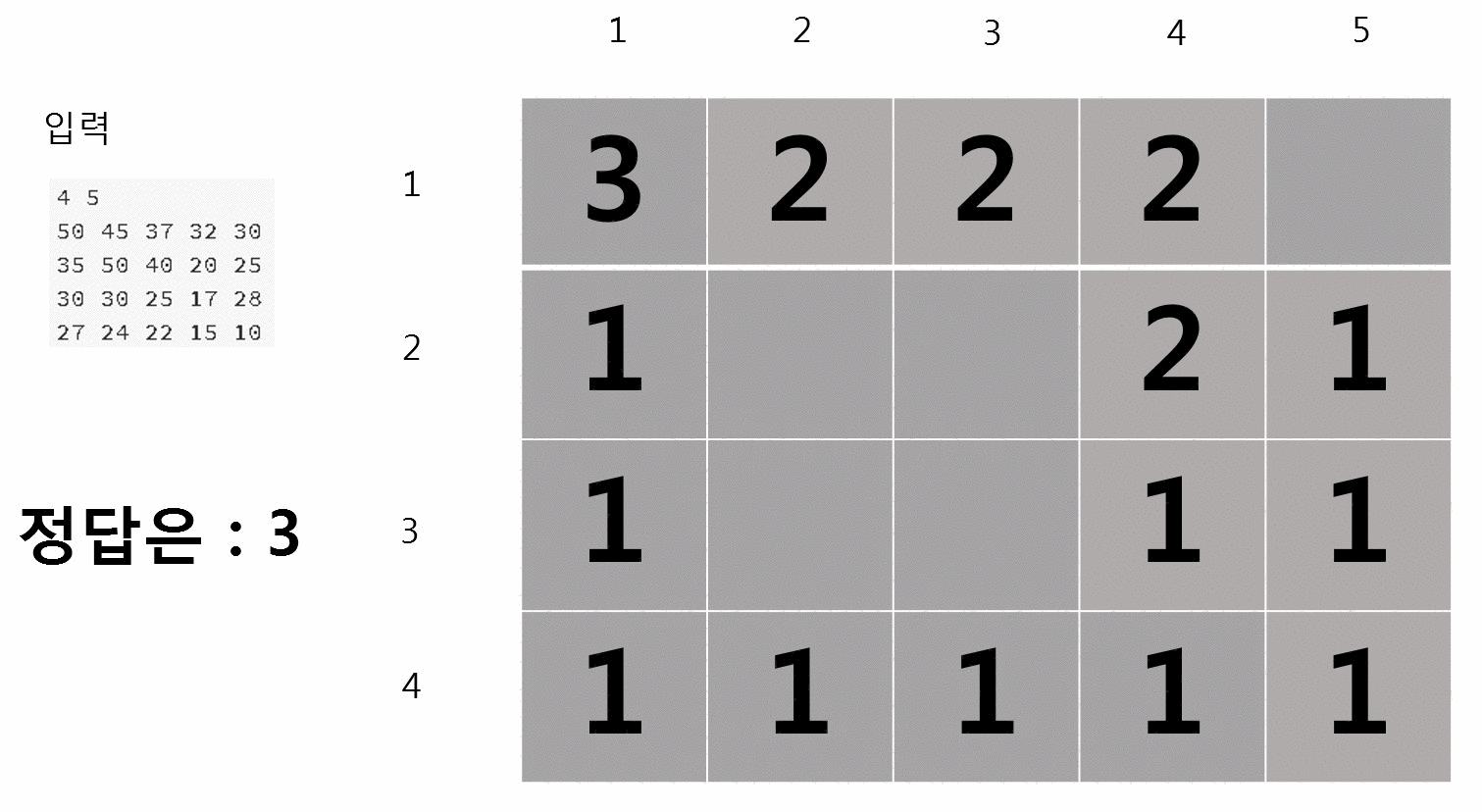
손수 애니메이션으로 만들어준 우투리와툴툴 티스토리 블로그님께 감사의 말씀을 전한다. 덕분에 이해하기가 쉽다.
5. 문제전략
문제 전략은 팩트 추출을 통해 알아보았다. DFS + DP 방식으로 문제를 풀었다.
6. 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int M, N;
static int[][] map;
static int[][] dp;
static int[] dx = { -1, 1, 0, 0 };
static int[] dy = { 0, 0, 1, -1 };
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
M = Integer.parseInt(st.nextToken());
N = Integer.parseInt(st.nextToken());
map = new int[M][N];
dp = new int[M][N];
for(int j = 0; j < M; j++) {
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
map[j][i] = Integer.parseInt(st.nextToken());
}
}
initDP();
System.out.println(dfs(0, 0));
}
private static void initDP() {
for(int j = 0; j < M; j++) {
for (int i = 0; i < N; i++) {
dp[j][i] = -1;
}
}
}
private static int dfs(int x, int y) {
if(x == M-1 && y == N-1){ return 1; }
if(dp[x][y] != -1) return dp[x][y];
dp[x][y] = 0;
for (int i=0; i<4; i++) {
int newX = x + dx[i];
int newY = y + dy[i];
if (newX < 0 || newX >= M || newY < 0 || newY >= N) continue;
if (map[x][y] <= map[newX][newY]) continue;
dp[x][y] += dfs(newX, newY);
}
return dp[x][y];
}
}'알고리즘 > BOJ' 카테고리의 다른 글
| [BOJ] N과 M (Java) (0) | 2022.09.27 |
|---|---|
| [BOJ] 11658 구간 합 구하기 3 (0) | 2022.08.31 |
| [BOJ] 10999 구간 합 구하기 2 (0) | 2022.08.30 |
| [BOJ] 9426 중앙값 측정 (0) | 2022.08.19 |
| [BOJ] 2138 전구와 스위치 (0) | 2022.08.17 |