1. Segment Tree
값이 변하는 연속 구간에 대한 정보를 저장할 때 사용하는 자료구조이다.
값이 변하지 않는다면 구간합을 한 번 연산하고, 계속 질의하면서 쿼리에 대한 결과값을 가져오면 되는데 중간에 있는 값이 변하게 된다면 다시 구간합을 구해야 하므로 O(N) 시간만큼 시간 복잡도가 발생하게 된다. 그래서 조회, 수정 시에도 O(lgN) 시간만큼 줄일 수 있는 자료구조가 필요했다.
일반적인 세그먼트 트리는 입력되는 값 범위의 트리 높이만큼 계산하기 때문에 (N개의 원소가 있을 때 구현에 따라) 2배에서 4배정도의 추가 공간이 필요하지만 원소의 변경, 특정 범위 내의 연산을 logN 에 수행할 수 있다는 장점이 있다.
데이터 관점에서 보면 트리는 아래처럼 구성된다.
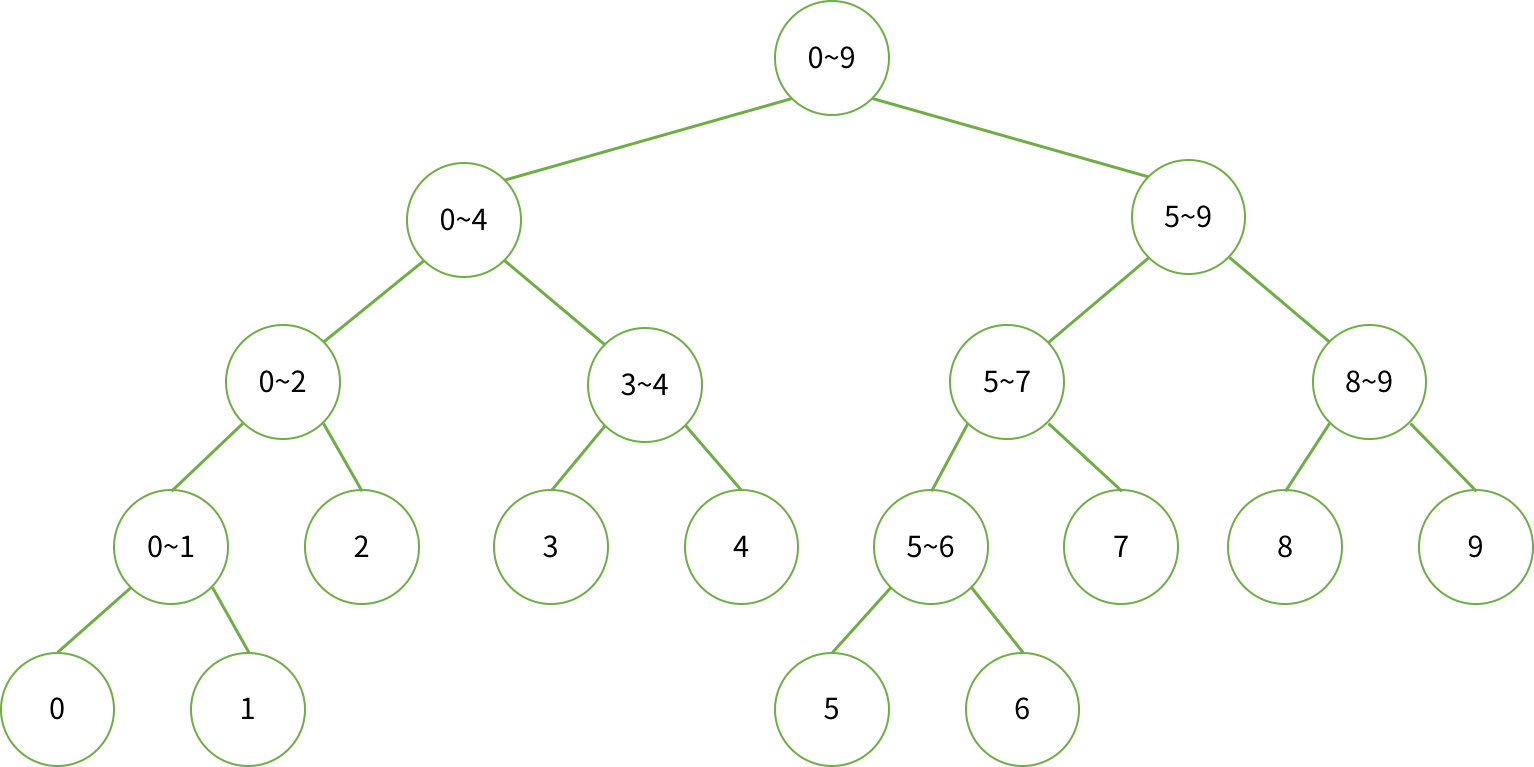
인덱스 관점에서 보면 트리는 아래처럼 구성된다.

트리의 인덱스가 0 이 아닌 1 인 이유는 1 부터 시작할 때 좌측부터 차례로 인덱스를 부여하면 아래 공식이 성립한다.
좌측 노드 인덱스 = 부모 노드 인덱스 * 2 (짝수)
우측 노드 인덱스 = 부모 노드 인덱스 * 2 + 1 (홀수)
반대로, 데이터는 1번 노드부터 전체 구간의 합이 적재되고, 내려오면서 반씩 범위가 쪼개져 그 구간의 합이 표시된다.
이진 탐색 트리 연산이므로 Top-Down 방식으로 이분할하여 데이터를 수정하고 조회하면 된다.
<템플릿>
class SegmentTree {
static long[] tree;
int treeSize;
public SegmentTree(int arrSize){
int h = (int) Math.ceil(Math.log(arrSize)/ Math.log(2));
this.treeSize = (int) Math.pow(2,h+1);
tree = new long[treeSize];
}
// 초기화와 수정을 update 에서 동시에
static void update(int node, int index, int updateValue, int left, int right) {
// 기저사례 (구간에 index 가 없는 경우)
if (index < left || index > right)
return;
// 기저사례 (마지막 구간에 index 가 있는 경우)
if (left == right) {
tree[node] = updateValue;
}
tree[node] += updateValue;
int mid = left + (right - left) / 2;
update(node * 2, index, updateValue, left, mid);
update(node * 2 + 1, index, updateValue, mid+1, right);
}
static void long query(int node, int startIndex, int endIndex, int left, int right){
// 기저사례 (구간에 쿼리구간이 없는 경우)
if (endIndex < left || startIndex > right)
return 0;
// 기저사례 (마지막 구간에 index 가 있는 경우)
if (endIndex >= right && startIndex <= left) {
return tree[node];
}
int mid = left + (right - left) / 2;
return query(node*2, startIndex, endIndex, left, mid) + query(node*2 + 1, startIndex, endIndex, mid+1, right);
}
}
2. Dynamic Segment Tree
일반적인 세그먼트 트리는 보통 입력 범위의 4배에 달하는 공간을 미리 할당한 후, 모두 업데이트한다. (위 세그먼트 트리 참고) 입력의 범위만큼 모든 영역(logN)을 업데이트해야 하며, 사용하지 않는 공간까지 낭비한다는 단점이 있다.
반면, Dynamic Segment Tree 는 이름에서도 알 수 있듯이 노드가 필요할 때만 생성해서 만들기 때문에 공간을 낭비하지 않는다. 값을 없데이트할 때 mid 노드의 자식 노드가 없는 경우 노드를 동적으로 생성해준다는 점이 다르다. 구간에 대한 쿼리 로직은 자식이 없는 경우만 예외처리해주면 일반적인 세그먼트 트리와 동일하다.
<템플릿>
static class SegmentTree {
static class Node {
long value;
Node leftChild, rightChild;
}
static Node getNode() {
Node temp = new Node();
temp.value = 0;
temp.leftChild = null;
temp.rightChild = null;
return temp;
}
static void initTree(Node node, int index, long updateValue, int left, int right) {
// 기저사례 (구간에 index 가 없는 경우)
if (index < left || index > right)
return;
// 기저사례 (마지막 구간에 index 가 있는 경우 (수정할 필요 없는 경우 값 셋팅))
// 초기화 과정이 없기 때문에 필요
if (left == right) {
node.value = updateValue;
return;
}
int mid = left + (right - left) / 2;
long leftSum = 0, rightSum = 0;
if (index <= mid) {
if (node.leftChild == null) {
node.leftChild = getNode();
}
update(node.leftChild, index, updateValue, left, mid);
} else {
if (node.rightChild == null) {
node.rightChild = getNode();
}
update(node.rightChild, index, updateValue, mid+1, right);
}
if (node.leftChild != null)
leftSum = node.leftChild.value;
if (node.rightChild != null)
rightSum = node.rightChild.value;
node.value = leftSum + rightSum;
}
static void updateRange(Node node, long updateValue, int updateStart, int updateEnd, int left, int right) {
// 기저사례 (구간에 쿼리구간이 없는 경우)
if (updateEnd < left || updateStart > right)
return;
int mid = left + (right - left) / 2;
updateRange(node.leftChild, updateValue, updateStart, updateEnd, left, mid);
updateRange(node.rightChild, updateValue, updateStart, updateEnd, mid + 1, right);
node.value = node.leftChild.value + node.rightChild.value;
}
static void int query(Node node, int startIndex, int endIndex, int left, int right){
// 기저사례 (할당되지 않은 경우)
if (node == null)
return 0;
// 기저사례 (구간에 쿼리구간이 없는 경우)
if (endIndex < left || startIndex > right)
return 0;
// 기저사례 (마지막 구간에 index 가 있는 경우)
if (endIndex >= right && startIndex <= left) {
return node.value;
}
int mid = left + (right - left) / 2;
return query(node.leftChild, startIndex, endIndex, left, mid) + query(node.rightChild, startIndex, endIndex, mid+1, right);
}
}
3. Dynamic Segment Tree (+ Lazy Propagation)
( 아무리 구글에 검색해봐도 메모리를 절약할 수 있는 Dynamic Segment Tree 와 연산을 줄이는 Lazy Propagation 을 같이 사용하는 코드가 없었다... 특히 Java 는 더욱 없었다. 그래서 내가 쓰려고 템플릿을 만들었다. )
Dynamic Segment Tree 에서 값을 업데이트할 때 자식노드들도 모두 변경하는데 굳이 지금 당장 자식노드의 조회나 수정이 필요 없는 경우라면 트리를 순회하면서 업데이트할 필요는 없다. lazy 라는 변수를 하나두고, 그 변수에 업데이트할 변수를 저장한 다음 나중에 조회하거나 수정할 때 한 단계씩 자식에게 전파하면 된다. 그래서 이름이 느린 전파이다.
업데이트 하고자 하는 범위를 updateStart, updateEnd 라고 할 때, 자식노드를 순회하면서 left, right 탐색 범위가 업데이트 하고자 하는 범위에 완전히 포함된다면 자식노드를 방문하지 않고 lazy 값만 자식노드에게 전파한뒤 종료한다. 자식 노드들을 방문하지 않는다.
<템플릿>
static class SegmentTree {
static class Node {
long value;
long lazy;
Node leftChild, rightChild;
}
static Node getNode() {
Node temp = new Node();
temp.value = 0;
temp.lazy = 0;
temp.leftChild = null;
temp.rightChild = null;
return temp;
}
static void updateLazy(Node node, int left, int right) {
// 만약 현재 노드에 lazy 값이 있다면
if (node.lazy != 0) {
// 만약 자식이 있다면 자식들에게 lazy 값을 전파한다.
if (node.leftChild != null) {
node.leftChild.lazy += node.lazy;
}
if (node.rightChild != null) {
node.rightChild.lazy += node.lazy;
}
// 현재노드 업데이트 ( 부모노드이므로 구간 길이만큼 업데이트 )
node.value += node.lazy * (right - left + 1);
// lazy 값을 업데이트했으므로 0으로 만들어준다.
node.lazy = 0;
}
}
// 초기화
static void initTree(Node node, int index, long updateValue, int left, int right) {
// 기저사례 (구간에 index 가 없는 경우)
if (index < left || index > right)
return;
// 기저사례 (마지막 구간에 index 가 있는 경우 (수정할 필요 없는 경우))
// 초기화 과정이 없기 때문에 필요
if (left == right) {
node.value = updateValue;
return;
}
int mid = left + (right - left) / 2;
long leftSum = 0, rightSum = 0;
if (index <= mid) {
if (node.leftChild == null) {
node.leftChild = getNode();
}
initTree(node.leftChild, index, updateValue, left, mid);
} else {
if (node.rightChild == null) {
node.rightChild = getNode();
}
initTree(node.rightChild, index, updateValue, mid + 1, right);
}
if (node.leftChild != null)
leftSum = node.leftChild.value;
if (node.rightChild != null)
rightSum = node.rightChild.value;
node.value = leftSum + rightSum;
}
static void updateRange(Node node, long updateValue, int updateStart, int updateEnd, int left, int right) {
updateLazy(node, left, right);
// 기저사례 (구간에 쿼리구간이 없는 경우)
if (updateEnd < left || updateStart > right)
return;
// 기저사례 (업데이트 구간이 완전히 포함되는 경우)
if (updateEnd >= right && updateStart <= left) {
node.value += (updateValue * (right - left + 1));
if (node.leftChild != null) {
node.leftChild.lazy += updateValue;
}
if (node.rightChild != null) {
node.rightChild.lazy += updateValue;
}
return;
}
int mid = left + (right - left) / 2;
updateRange(node.leftChild, updateValue, updateStart, updateEnd, left, mid);
updateRange(node.rightChild, updateValue, updateStart, updateEnd, mid + 1, right);
node.value = node.leftChild.value + node.rightChild.value;
}
static long query(Node node, int queryStart, int queryEnd, int left, int right) {
updateLazy(node, left, right);
// 기저사례 (할당되지 않은 경우)
if (node == null)
return 0;
// 기저사례 (구간에 쿼리구간이 없는 경우)
if (queryEnd < left || queryStart > right)
return 0;
// 기저사례 (쿼리 구간이 완전히 포함되는 경우)
if (queryEnd >= right && queryStart <= left) {
return node.value;
}
int mid = left + (right - left) / 2;
return query(node.leftChild, queryStart, queryEnd, left, mid) + query(node.rightChild, queryStart, queryEnd, mid + 1, right);
}
}
Q . updateRange 와 Query 함수에서 updateLazy 를 가장 먼저 호출해야 되는 이유?
A . 해당 템플릿이 완성되기 전, 구간에 쿼리 구간이 없는 경우 updateLazy 를 할 필요가 없지 않나? 라고 생각했었다. 그래서 "기저사례 (구간에 쿼리구간이 없는 경우)" 로직 뒷 부분에 updateLazy 를 배치하고 최적화를 잘 했다며 만족했었다.
그런데, Lazy Propagation 의 대표문제인 백준 10999 문제를 풀어보니 모두 틀렸다고 나오는 것이었다. 게시판에서 언급하고 있는 반례 케이스들은 모두 맞았는데 안 되니까 답답할 노릇이었다. 잘 생각해보면 잘못된 생각이었다.
만약 부모 노드에 lazy 값이 있는데 자식 노드가 범위를 벗어난다면 lazy 를 전파받지 못하고 계산이 되기 때문이다. 꼭 query 와 update 할 때 updateLazy 를 먼저 호출하자.
'알고리즘 > 개념' 카테고리의 다른 글
| [알고리즘] BFS & DFS (0) | 2022.07.12 |
|---|---|
| [알고리즘] 투 포인터 알고리즘 (Two Pointer) (0) | 2022.06.29 |
| [알고리즘] LCA (Lowest Common Ancestor) (0) | 2022.05.04 |
| [알고리즘] DP (Dynamic Programming) (0) | 2021.05.10 |
