1. 문제요약
13334번: 철로
입력은 표준입력을 사용한다. 첫 번째 줄에 사람 수를 나타내는 양의 정수 n (1 ≤ n ≤ 100,000)이 주어진다. 다음 n개의 각 줄에 정수 쌍 (hi, oi)가 주어진다. 여기서 hi와 oi는 −100,000,000이상, 100,000,0
www.acmicpc.net
집과 사무실의 시작점, 끝점과 주어진 길이 d 가 주어질 때, 길이 d 에 포함되는 집과 사무실 구간의 개수가 최대인 경우를 구하시오.
2. 문제예제
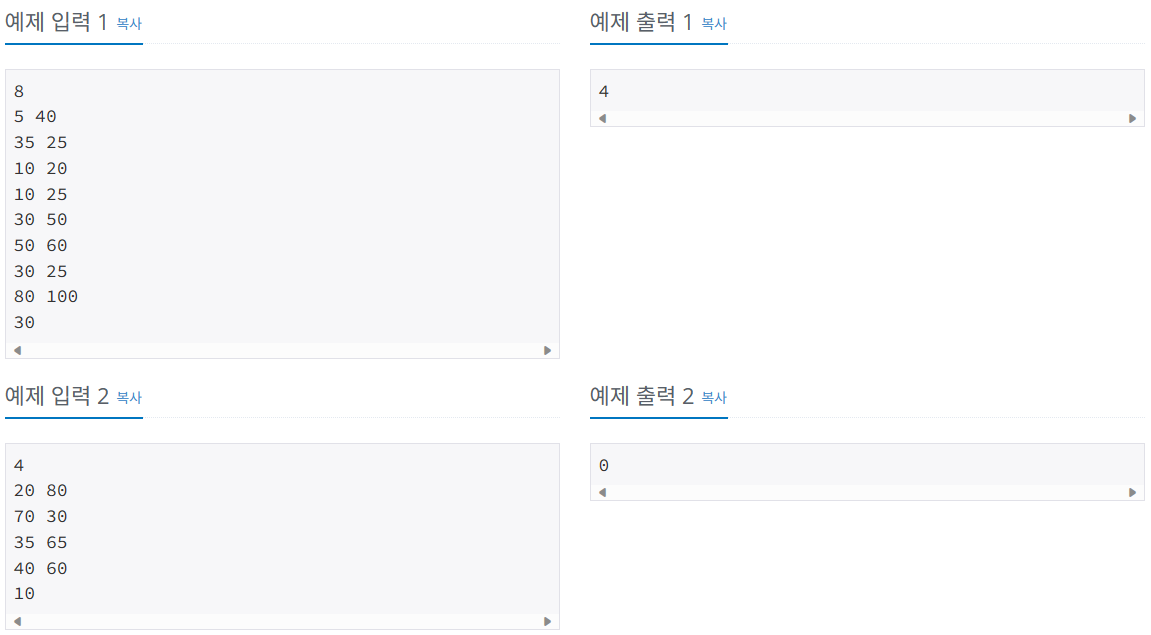
3. 문제풀이(수동)
예제들을 문제풀이하면서 아이디어를 얻을 수는 없다. 아래 팩트추출을 통해 모든 경우의 수를 점검해야 한다.
4. 팩트추출
Fact 1 : 범위가 포함이 되어있는지 확인할 때, 나머지 좌표들을 정렬하면 다른 한 쪽만 대소비교할 수 있어 복잡도를 줄일 수 있다. 아래는 구간들의 오른쪽 끝점을 기준으로 오름차순으로 정렬한 모습이다. 가장 아래쪽부터 1번, 2번, 3번이라고 지칭할 때 다양한 특징들이 발견된다.

먼저 1번을 기준으로 2번이 포함되지 않는다면 3번, 4번에서도 2번은 포함되지 않는다. (오른쪽 끝점이 계속 순차적으로 증가하는 형태이기 때문에) 한 번 제외된 구간은 다른 구간에서 계산할 때도 제외된다는 뜻이다.
Fact 2 : 거리 N 에 포함되지 않는 구간은 계산할 필요가 없다.
Fact 3 : 이전 결과에서는 거리 N 에 포함이 되었더라도 다음에 계산할 때는 오른쪽 끝점이 이동하므로 포함되지 않을 수 있다. 이전 결과를 활용하기 위해 시작점도 정렬이 필요하다. 거리 N 에 포함되면 시작점을 포함했다가 오른쪽 끝점이 이동할 때 정렬되어 있는 시작점들에서 하나씩 꺼내 비교하면 모두 다 비교하지 않아도 된다.
5. 문제전략
한 쪽을 정렬해서 이전 결과 값을 재활용해야 한다는 점, 다른 한 쪽도 삽입을 하면서 정렬을 해야한다는 점을 파악해야 한다. 삽입하면서 정렬하는 자료구조는 우선순위큐가 적절하다.
5. 소스코드
private static class Interval implements Comparable<Interval> {
int start, end;
Interval(int startVariable, int endVariable) {
start = startVariable;
end = endVariable;
}
@Override
public int compareTo(Interval o) {
return Integer.compare(this.end, o.end);
}
}
public static void main(String[] args) {
// 거리 N, Interval 은 집과 구간, 오른쪽 끝점으로 정렬
// ... (생략) ...
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (Interval interval : intervals) {
if (interval.start >= interval.end - N) {
count++;
pq.add(interval.start);
}
while (!pq.isEmpty() && pq.peek() < interval.end - N) {
pq.poll();
count--;
}
maximum = Math.max(maximum, count);
}
}
'알고리즘 > BOJ' 카테고리의 다른 글
| [BOJ] 1715 카드 정렬하기 (Java) (0) | 2023.11.18 |
|---|---|
| [BOJ] 24042 횡단보도 (Java) (0) | 2022.10.12 |
| [BOJ] 10830 행렬 제곱 (Java) (0) | 2022.10.03 |
| [BOJ] 9376 탈옥 (Java) (0) | 2022.10.02 |
| [BOJ] 이항 계수 (Java) (0) | 2022.09.29 |